上采样(upsampling) 作者:马育民 • 2020-02-22 23:47 • 阅读:11767 # 介绍 上采样(upsampling),主要目的是放大原图像 对图像的放大操作不能带来更多关于该图像的信息, 因此图像的质量将不可避免地受到影响。 但使用一些算法可以增加图像的信息,从而使得缩放后的图像质量超过原图质量的。 # 深度学习中的上采样 主要有三种方式: - 插值法 (Interpolation) - 反池化 (unPooling) 。 - **反卷积 (Deconvolution) ** # 插值法 在原有图像像素的基础上,在像素点之间采用合适的插值算法插入新的元素。 插值就是在不生成像素的情况下增加图像像素大小的一种方法,在周围像素色彩的基础上用数学公式计算丢失像素的色彩(也有的有些相机使用插值,人为地增加图像的分辨率)。 所以在放大图像时,图像看上去会比较平滑、干净。但必须注意的是插值并不能增加图像信息。 ### 分类 目前分类比较混乱,说法不一 文献《图像插值技术综述》中将插值算法分为: - 传统插值 如:双线性插值(bilinear ) - 基于边缘图像的插值 - 基于区域的图像插值 各种插值方法都有各自的优缺点。 ### 常用的插值算法 常用的插值算法有很多 - 最邻近插值(Nearest Neighbour Interpolation) - 双线性插值(Bilinear Interpolation) - 双三次插值算法(Bicubic Interpolation) 双线性插值的改进算法 - 等等 ### 最邻近插值(Nearest Neighbour Interpolation) 简单,常用在图片放大,效果不好,会有色块 [](https://www.malaoshi.top/upload/0/0/1EF52Fns8kxv.png) [代码参考请点击](https://cloud.tencent.com/developer/article/1338324 "代码参考") ### 双线性插值(Bilinear Interpolation) 双线性插值是目前在 **语义分割** 中用的比较多的一种方式 如下图:已知Q12、Q22、Q11、Q21这四个点的坐标和像素值,P点是要插入的像素,求P点的像素值 [](https://www.malaoshi.top/upload/0/0/1EF52HsCtWeN.png) 算法复杂、计算量大、但极大地消除了锯齿现象 # 反池化(unpooling) 出自2013年纽约大学Matthew D. Zeiler和Rob Fergus发表的《Visualizing and Understanding Convolutional Networks》 论文:https://arxiv.org/abs/1311.2901 ### max unpooling 在池化过程中,记录下max-pooling在对应kernel中的坐标,在反池化过程中,将一个元素根据kernel进行放大,根据之前的坐标将元素填写进去,**其他位置补0**。 [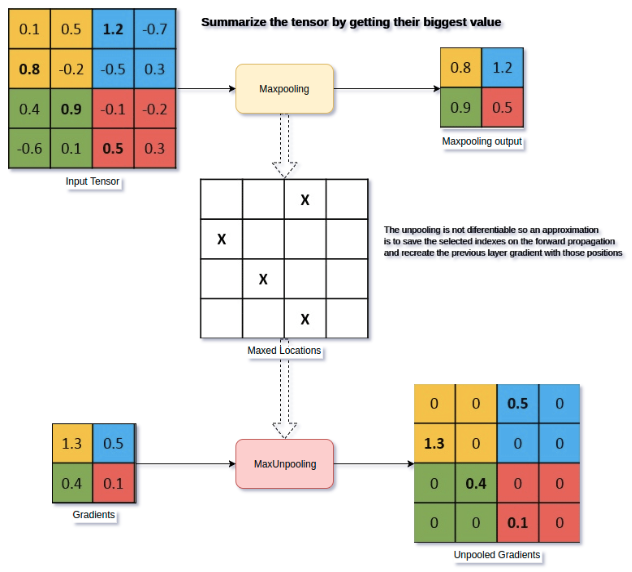](https://www.malaoshi.top/upload/0/0/1EF52H0ImMxK.png) [图出处](https://www.oreilly.com/library/view/hands-on-convolutional-neural/9781789130331/6476c4d5-19f2-455f-8590-c6f99504b7a5.xhtml "图出处") **注意:** 上图中,左下角的图,是右上角的图,进行梯度计算后的结果 在CNN中常用的来表示max pooling的逆操作。 在SegNet神经网络中用到 # 反卷积(Deconvolution ) 参见: https://www.malaoshi.top/show_1EF52HLXBmqf.html # keras 有UnSampling和反卷积的api - tf.keras.layers.UpSampling2D - tf.keras.layers.Conv2DTranspose # 感谢 https://blog.csdn.net/stf1065716904/article/details/78450997 https://www.cnblogs.com/han1ning1/p/6924404.html https://blog.csdn.net/majinlei121/article/details/46742339 https://www.cnblogs.com/xpvincent/archive/2013/03/15/2961448.html https://blog.csdn.net/weixin_43206928/article/details/88964128 原文出处:http://malaoshi.top/show_1EF52HM7gu6g.html