数据结构:二叉搜索树的高度 作者:马育民 • 2022-07-06 10:23 • 阅读:10135 # 说明 N个结点的二叉搜索树,高度是 `log2(N) + 1` (取整数,丢弃小数,不是四舍五入) [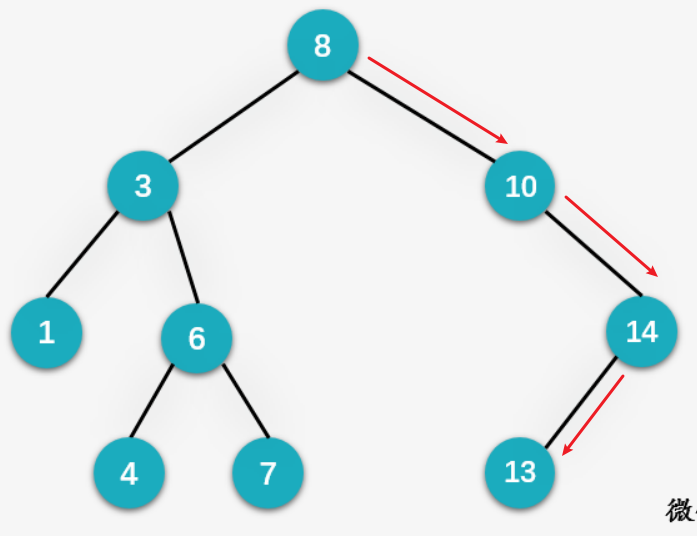](/upload/0/0/1IX3cKBTAb4J.png) # 计算过程 ### 1个根节点的二叉搜索树高度 高度为1,计算过程: ``` 第一步: log2(1)=0 第二步: 0+1=1 ``` ### 2个结点的二叉搜索树高度 高度为2,计算过程: ``` 第一步: log2(2)=1 第二步: 1+1=2 ``` ### 3个结点的二叉搜索树高度 高度为2,计算过程: ``` 第一步: log2(3)=1.58,取整是 1 第二步: 1+1=2 ``` ### 7个结点的二叉搜索树高度 高度为3,计算过程: ``` 第一步: log2(7) = 2.80,取整是 2 第二步: 2+1=3 ``` ### 结论 N个结点的二叉搜索树,高度是[log2(N)]+1。[]表示取整。 # 退化成链表 当数据,按照 **顺序存放** 时,如下: ``` 存放 2、3、5、7、8 ``` 会退化成 **链表** ,如下: [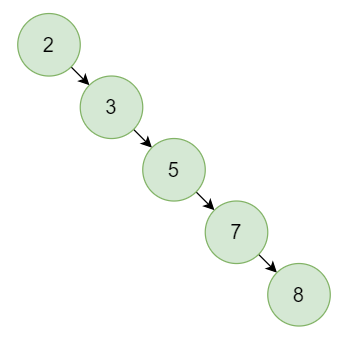](/upload/0/0/1IX3ctMvE3FP.png) 此时,5个节点,高度是 5 先说说最好情况,最好情况就是,要查找的那个数刚好是根节点,只需要查找1次。最坏情况,要查找到树的最深节点,查找次数是树的高度。根据上面所讲,树的高度就是[log2(n)]+1。 我们平常所说的时间复杂度,是指最坏时间复杂度。因为平均时间复杂度和最坏时间复杂度很接近,所以就直接考虑最坏时间复杂度。对这一点有疑问,参考:算法(一)时间复杂度。 由此,我们可以确定O(n)=[log2(n)]+1 #### 参考 https://blog.csdn.net/zhangjin1120/article/details/121237377 原文出处:http://malaoshi.top/show_1IX3ctTefutk.html