多项式朴素贝叶斯-python sklearn实现-马育民老师

# 介绍

多项式朴素贝叶斯主要适用于 **离散特征** 的概率计算，用于解决 **多分类** 问题

**注意：** sklearn的多项式模型不接受输入负值。

### 应用场景

多项式朴素贝叶斯多用于 **文档分类**，它可以计算出一篇文档为某些类别的概率，最大概率的类型就是该文档的类别。

举个例子，比如判断一个文档属于体育类别还是财经类别，那么只需要判断P(体育|文档)和P(财经|文档)的大小。

而文档中其实就是一个个关键词（提取出的文档关键词），所以我们需要计算的P(体育|词1，词2，词3......)和P(财经|词1，词2，词3.....)。

我们之前求得都是一个条件下多类别的公式

# 例子

下图中的训练集中一共有30篇科技文章，60篇娱乐文章，共计90篇文章。这些文章中根据tf-idf提取出重要的词语分别有商场、影院、支付宝和云计算，并统计了在不同类别文章中出现的次数：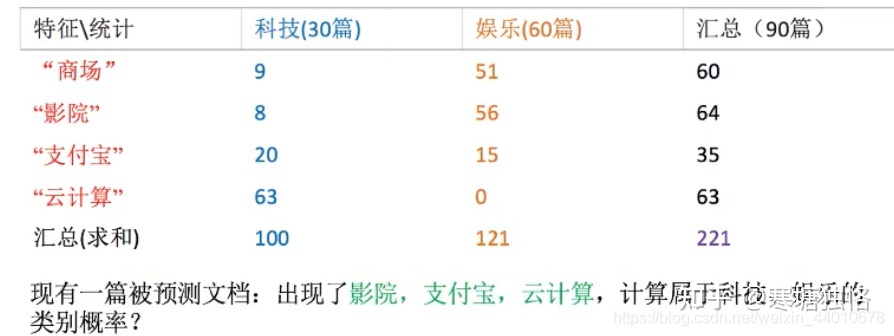

[![](/upload/0/0/1IX4lp6BI2ng.jpg)](/upload/0/0/1IX4lp6BI2ng.jpg)

套入到下面朴素贝叶斯的公式：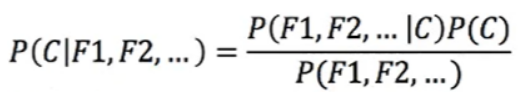

[![](/upload/0/0/1IX4lp1rbuPQ.png)](/upload/0/0/1IX4lp1rbuPQ.png)

**解释：**

- C为文档的类别（财经，体育，军事......）
- F1，F2为文档中的关键词

带入式子中进行计算：
```
P(科技|影院，支付宝，云计算)=
P(影院，支付宝，云计算|科技)*P(科技)=
(8/100)(20/100)(63/100)(30/90)=0.005
```
```
P(娱乐|影院，支付宝，云计算)=
P(影院，支付宝，云计算|娱乐)*P(娱乐)=
(56/121)(15/121)(0/121)(60/90)=0
```

## 提出问题

由上面可知，预测文章属于 **娱乐** 的 **概率为0**，肯定不合适，**不能因为一个词不出现而否定了其他关键词**

这就需要引入 **拉普拉斯平滑系数**

## 解决问题：拉普拉斯平滑系数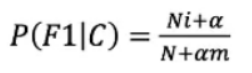

[![](/upload/0/0/1IX4lpEAxnQ6.png)](/upload/0/0/1IX4lpEAxnQ6.png)

**参数解释：**

- `a`：是指定的系数，一般为1
- `m`：是训练文档中统计出的特征词个数
- `Ni`：原来 `P(F1|C)` 中的分子
- `N`：原来 `P(F1|C)` 中的分母

那么原来的式子就变成了：
```
P(科技|影院，支付宝，云计算)=
P(影院，支付宝，云计算|科技)*P(科技)=
((8+1)/(100+1*4))((1+20)/(100+1*4))((1+63)/(100+1*4))(30/90)
```
```
P(娱乐|影院，支付宝，云计算)=
P(影院，支付宝，云计算|娱乐)*P(娱乐)=
((1+56)/(121+1*4))((1+15)/(121+1*4))((1+0)/(121+1*4))(60/90)
```

这样就不会出现等于0的情况了。

# API 声明

```
class sklearn.naive_bayes.MultinomialNB(
    alpha=1.0,
    fit_prior=True,
    class_prior=None
)
```

**参数解释：**

- alpha:拉普拉斯平滑系数，默认为1.0。注意拉普拉斯平滑系数不是超参数，并不会影响最后的结果。

- fit_prior : 布尔值, 可不填 (默认为True)
是否学习先验概率 `P(Y=c)`。如果设置为false，则不使用先验概率，而使用统一先验概率（uniform prior），即认为每个标签类出现的概率是 `1 / n_classes`

- class_prior：形似数组的结构，结构为(n_classes, )，可不不填（默认为None）
类的先验概率P(Y=c)。如果没有给出具体的先验概率则自动根据数据来进行计算。

# 使用例子

### 训练模型、预测

```
import numpy as np
from sklearn.naive_bayes import MultinomialNB

# 测试数据
X = np.array([[2,1,1,3,3],[2,0,2,1,1],[0,2,1,0,4],[1,0,3,1,3],[1,3,3,3,2]])
# 测试标签
y = np.array([1, 2, 3, 4, 5])
clf = MultinomialNB()

# 训练模型
clf.fit(X, y)

# 预测
print(clf.predict(X[2:3]))
```

执行结果：

```
[3]
```

### class_prior 参数

若指定了 `class_prior` 参数，不管 `fit_prior` 为 `True` 或 `False`，`class_log_prior_` 取值是 `class_prior` 转换成log后的结果

```
import numpy as np
from sklearn.naive_bayes import MultinomialNB
X = np.array([[2,1,1,3,3],[2,0,2,1,1],[0,2,1,0,4],[1,0,3,1,3],[1,3,3,3,2]])
y = np.array([1, 2, 3, 4, 5])
clf = MultinomialNB()
clf.fit(X, y)
## 观察各类标记的平滑先验概率对数值
print(clf.class_log_prior_)
## 指定先验概率
clf1 = MultinomialNB(alpha=1.0,fit_prior=False,class_prior=[0.3,0.2,0.1,0.2,0.2])
clf1.fit(X,y)
## 观察各类标记的平滑先验概率对数值
print(clf1.class_log_prior_)
```

执行结果：

```
[-1.60943791 -1.60943791 -1.60943791 -1.60943791 -1.60943791]
[-1.2039728  -1.60943791 -2.30258509 -1.60943791 -1.60943791]
```

### fit_prior 参数为 False

若 `fit_prior` 参数为 `False`，`class_prior=None`，则各类标记的先验概率相同等于类标记总个数N分之一

# 验证是否是1/5
print(np.log(0.2))
```

执行结果：

```
[-1.60943791 -1.60943791 -1.60943791 -1.60943791 -1.60943791]
-1.6094379124341003
```

### fit_prior参数为True

若 `fit_prior` 参数为 `True`，`class_prior=None`，则各类标记的先验概率等于各类标记个数除以各类标记个数之和（将y的类别稍加改动即可）

```
import numpy as np
from sklearn.naive_bayes import MultinomialNB
X = np.array([[2,1,1,3,3],[2,0,2,1,1],[0,2,1,0,4],[1,0,3,1,3],[1,3,3,3,2]])
y = np.array([1, 1, 2, 3, 4])
clf = MultinomialNB(fit_prior=True,class_prior=None)
clf.fit(X, y)
## 观察各类标记的平滑先验概率对数值
print(clf.class_log_prior_)

# 验证是否是2/5 、 1/5 、1/5 、1/5
print(np.log(2/5),np.log(1/5),np.log(1/5),np.log(1/5))
```

输出：

```
[-0.91629073 -1.60943791 -1.60943791 -1.60943791]
-0.916290731874155 -1.6094379124341003 -1.6094379124341003 -1.6094379124341003
```

参考：
https://zhuanlan.zhihu.com/p/386815121
https://blog.csdn.net/weixin_43999327/article/details/99554549

原文出处：http://malaoshi.top/show_1IX4ltExZ8YY.html