空洞卷积（Atrous Convolution）-马育民老师

# 介绍

**空洞卷积**，又称 带孔卷积（Atrous Convolution），又称 扩张卷积/膨胀卷积（Dilated Convolutions）

出处：[Multi-Scale Context Aggregation by Dilated Convolutions](https://arxiv.org/abs/1511.07122 "Multi-Scale Context Aggregation by Dilated Convolutions")

# 作用
在出现空洞卷积之前的CNN分割网络中，习惯于使用Pooling的方式降低图像的尺寸，同时增大网络的 **感受野**。
最后再使用Upsampling操作将图像的尺寸恢复到原始的大小，以得到像素级的分割结果。

这样的一个 Pooling->Upsampling 的操作导致图像的一些信息丢失(Pooling不可逆)，尤其在细节上可能会有比较大的影响。
所以为了达到 **增大感受野** 同时 **不丢失图像信息** 的效果，提出了空洞卷积

# 卷积 vs 空洞卷积

### 卷积

计算公式：
- S是strides（滑动步长）
- 原图片大小为N1xN1（下图为4x4）
- 卷积核大小为N2xN2（下图为3x3）
- P是padding大小

卷积后图像大小：`(N1-N2+2P)/S+1`

如下图：
[![](https://www.malaoshi.top/upload/0/0/1EF52IpmOtMl.gif)](https://www.malaoshi.top/upload/0/0/1EF52IpmOtMl.gif)

### 空洞卷积

空洞卷积（Atrous convolutions）在卷积时，在卷积核元素之间插入0值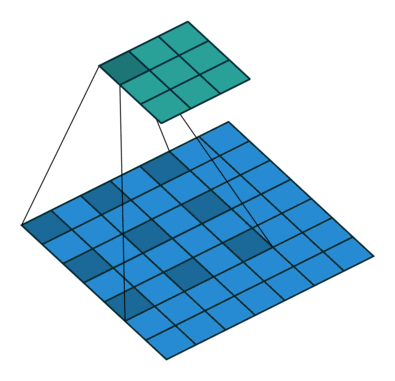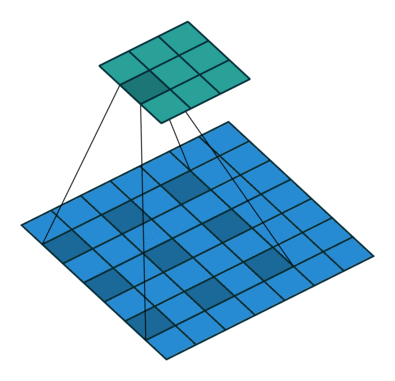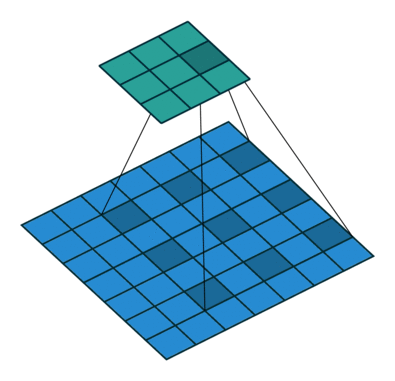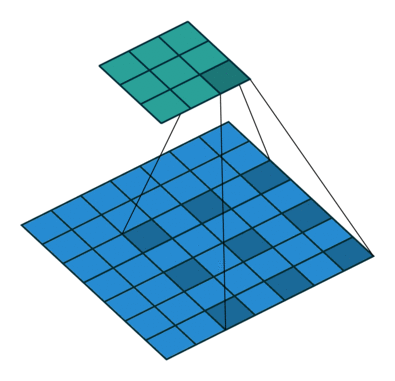

[![](https://gitee.com/65242847/images/raw/master/gif/dilation.gif)](https://gitee.com/65242847/images/raw/master/gif/dilation.gif)

引入了一个新的超参数 d，插入的0值数量：(d - 1)，假设原来的卷积核大小为 k，那么插入了 (d - 1) 个0值后的卷积核大小 n 为：
```
n=k+(k-1)*(d-1)
```

空洞卷积结果大小计算公式为：
- S是strides（滑动步长）
- 原图片大小为N1xN1（上图为7x7）
- 卷积核大小为N2xN2（上图为3x3）
- P是padding大小（上图为0）

```
(N1-n+2p)/S+1
```

代入式子：

空洞卷积核大小为：
```
n=N2+(N2-1)*(d-1) = 3+(3-1)*(2-1)=5
```

空洞卷积结果大小为：
```
(N1-n+2p)/S+1 = (7-5+2*0)/1+1 = 3
```

感谢：https://www.jianshu.com/p/09ea4df7a788

原文出处：http://malaoshi.top/show_1EF56ggAUmQ8.html